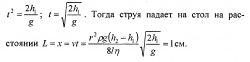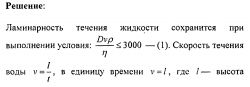4.16. В боковую поверхность сосуда вставлен горизонтальный капилляр, внутренний радиус которого r = 1 мм и длина l = 1,5 см. В сосуд налит глицерин, динамическая вязкость которого n = 1,0 Па с. Уровень глицерина в сосуде поддерживается постоянным на высоте h = 0,18м выше капилляра. Какое время потребуется на то, чтобы из капилляра вытек объем глицерина V = 5 см3? 4.17. На столе стоит сосуд, в боковую поверхность которого вставлен горизонтальный капилляр на высоте h, = 5 см от дна сосуда. Внутренний радиус капилляра r = 1 мм и длина l = 1см. В сосуд налито машинное масло, плотность которого р = 0,9 • 10J кг/м3 и динамическая вязкость n = 0,5 Па с. Уровень масла в сосуде поддерживается постоянным на высоте h2 = 50 см
выше капилляра. На каком расстоянии L от конца капилляра (по горизонтали) струя масла падает на стол? 4.18. Стальной шарик падает в широком сосуде, наполненном трансформаторным маслом, плотность которого р = 0,9 • 103 кг/м3 и динамическая вязкость n = 0,8Па с. Считая, что закон Стокса имеет место при числе Рейнольдса Re < 0,5 (если при вычислении Re в качестве величины D взять диаметр шарика), найти предельное значение диаметра D шарика.4.19. Считая, что ламинарность движения жидкости (или газа) в цилиндрической трубе сохраняется при числе Рейнольдса Rе<3000 (если при вычислении Re в качестве величины D взять диаметр трубы), показать, что условия задачи 4.1 соответствуют ламинарному движению. Кинематическая вязкость газа v = 1,33 • Ю*-6 м2/с.4.20. Вода течет по трубе, причем за единицу времени через поперечное сечение трубы протекает объем воды Vt = 200 см3/с. Динамическая вязкость воды n = 0,001 Пас. При каком предельном значении диаметра D трубы движение воды остается ламинарным? (Смотри условие предыдущей задачи.)
выше капилляра. На каком расстоянии L от конца капилляра (по горизонтали) струя масла падает на стол? 4.18. Стальной шарик падает в широком сосуде, наполненном трансформаторным маслом, плотность которого р = 0,9 • 103 кг/м3 и динамическая вязкость n = 0,8Па с. Считая, что закон Стокса имеет место при числе Рейнольдса Re < 0,5 (если при вычислении Re в качестве величины D взять диаметр шарика), найти предельное значение диаметра D шарика.4.19. Считая, что ламинарность движения жидкости (или газа) в цилиндрической трубе сохраняется при числе Рейнольдса Rе<3000 (если при вычислении Re в качестве величины D взять диаметр трубы), показать, что условия задачи 4.1 соответствуют ламинарному движению. Кинематическая вязкость газа v = 1,33 • Ю*-6 м2/с.4.20. Вода течет по трубе, причем за единицу времени через поперечное сечение трубы протекает объем воды Vt = 200 см3/с. Динамическая вязкость воды n = 0,001 Пас. При каком предельном значении диаметра D трубы движение воды остается ламинарным? (Смотри условие предыдущей задачи.)